 |
Gespanntes Seil um den Äquator der Erde
Fragen und Bemerkungen gerne an: werner.brefeld@web.de, Adresse: siehe Impressum,
Themenübersicht auf der Hauptseite:
Mathematik im Alltag, verblüffende Mathematik-Rätsel, Stochastik und Polyeder, irdisches und außerirdisches Leben
|
13. Ein Seil wird straff um den Äquator gespannt und anschließend um 1 Meter verlängert.
Wie hoch kann man das Seil nun an einer Stelle ziehen, bis es wieder straff wird, wenn man für den Radius der Erde
eine Länge von 6378 km annimmt?
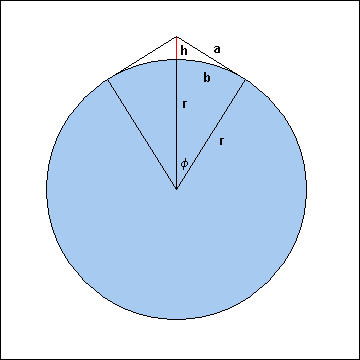
Die Höhe von der Spitze des Seils bis zum Erdboden sei h, r sei der Radius der Erde und a der Abstand von der
Seilspitze bis zum Punkt, an dem das Seil die Erde zum ersten Mal wieder berührt. Die Großkreisentfernung
von diesem Punkt bis zum Fußpunkt unter der Seilspitze sei mit b bezeichnet. φ sei der Winkel zwischen
den Verbindungen von Erdmittelpunkt zur Seilspitze und von Erdmittelpunkt zum Berührungspunkt.
Dann gilt:
tan(φ) = a / r und φ = b / r
Subtrahiert man die zweite Gleichung von der ersten, erhält man:
tan(φ) – φ = (a – b) / r = 0,5 m / 6.378.000 m = 1/12.756.000
Für a – b muss man die Hälfte der Seilverlängerung s von 1 Meter einsetzten, weil sich diese auf jede
der beiden Seiten des abfallenden Seils gleichmäßig aufteilt. Leider kann man die letzte Gleichung mit
dem Winkel φ nicht analytisch lösen. Deshalb muss man die numerische Lösung durch
Iteration gewinnen. Die anschaulichste Iterationsmethode läuft darauf hinaus, dass man
zwei Winkel sucht, bei denen das Ergebnis einmal zu klein und einmal zu groß ausfällt.
Der Wert für die Winkel muss dabei in Bogenmaß ausgedrückt werden.
Man kann zum Beispiel mit φ = 0 und φ = 1 beginnen. Dann bildet man das arithmetische
Mittel der beiden Winkel, also 1/2, und bestimmt dafür das Ergebnis. Daraus lässt sich sofort
schließen, ob die gesuchte Lösung zwischen 0 und 1/2 oder zwischen 1/2 und 1 liegt.
Das entsprechende Intervall wird wieder halbiert und das Verfahren entsprechend fortgesetzt.
Der Bereich, in dem die Lösung für φ liegt, wird also mit jedem Schritt halbiert.
Man kann aufhören, wenn man die gewünschte Genauigkeit erreicht hat. Die auf 6 signifikante
Ziffern genaue Lösung lautet:
φ = 0,00617258 = 0,3536628°
Mit Hilfe von φ lässt sich nun h und b analytisch berechnen. Es gilt:
cos(φ) = r / (r + h)
Die gesuchte Höhe h ergibt sich dann nach Umformen dieser Gleichung und Einsetzen von r und φ:
h = r · (1 / cos(φ) – 1) = 121,505 m
Außerdem gilt für die Großkreisentfernung b:
b = r · φ = 39.369 m
Man kann das Seil also erstaunliche 121,505 Meter hochheben und der Fußpunkt ist von
den Punkten, an denen das Seil zum ersten Mal die Erde berührt, fast 40 km entfernt.
Was ist verblüffend an diesem Mathematik-Rätsel? Intuitiv glauben viele, nach einer Verlängerung
um einen Meter könne man das Seil nicht mal einen Meter hochziehen, weil das Seil dann ja einen Meter
nach oben und dann auch noch wieder einen Meter nach unten muss.
Wenn man den Aufwand scheut, über die oben beschriebene Iteration zur exakten Lösung zu gelangen,
kann man auch auf anderem Wege schneller zu einem sehr genauen Ergebnis kommen.
Dazu nutzt man aus, dass sich der Tangens als Potenzreihe darstellen lässt, also
als eine unendliche Summe von Ausdrücken, bei denen nur Potenzen des Winkels auftreten.
Ist φ sehr viel kleiner als 1, was ja hier der Fall ist, stellen schon die ersten
beiden Summanden dieser Potenzreihe eine sehr gute Näherung dar:
tan(φ) = φ + 1/3 · φ3
Nach Einsetzten in die obige Gleichung ergibt sich:
φ3 = 3 · (a – b) / r = 3/2 · s / r
und für φ:
φ = (3/2 · s / r)1/3
Ebenso lässt sich für kleine Werte von φ der cos(φ) angenähert ausdrücken als:
cos(φ) = 1 – φ2/2
Eingesetzt in die Gleichung für h ergibt:
h = r · (1 / (1 – φ2/2) – 1)
Weil 1 / (1 – x) für x << 1 ungefähr gleich 1 + x ist, führt diese letzte Näherung zu:
h = r · (1 + φ2/2 – 1) = 1/2 · r · φ2
Das Einsetzen von φ ergibt dann die endgültige Näherungsformel für die Höhe:
h = 1/2 · r · φ2 = 1/2 · r · (3/2 · s / r)2/3 = (9/32 · r · s2)1/3
Für die Höhe erhält man wie oben den gleichen Wert von 121,505 m. Die Abweichung zur exakten Formel ist also geringer als 1 mm.
Aber diese Näherungsformel gilt nur, solange der Radius der betrachteten Kugel sehr viel größer ist als die Seilverlängerung.
Zum Schluss sei noch kurz die einfache Variante dieses Rätsels erwähnt: Wie weit steht das Seil von der Erde ab, wenn man
es nicht an einer Stelle, sondern überall gleichmäßig und gleichzeitig hochzieht?
Der Umfang U der Erde beträgt: U = 2 · π · r
Die Länge L des verlängerten Seils ist dann: L = U + 1 m = 2 · π · r + 1 m
Nach dem Hochziehen ist das Seil wieder kreisförmig. Der Radius rs dieses Kreises ist:
rs = L / (2 · π) = (2 · π · r + 1 m) / (2 · π) = r + 1 m / (2 · π)
Die Differenz der beiden Radien ist dann die Höhe über der Erdoberfläche, in der sich das abstehende Seil überall befindet:
rs – r = r + 1 m / (2 · π) – r = 1 m / (2 · π) = 15,9 cm
Um diese verblüffend große Strecke von etwa 15,9 cm steht das Seil demnach überall von der Erdoberfläche ab.
Das Ergebnis ist immer das gleiche, unabhängig von der Größe der Kugel.
Die Web-Seite Gespanntes Seil vom Nordpol zum Südpol der Erde beschreibt ein ähnliches, aber einfacheres
Mathematikrätsel.
Copyright © Werner Brefeld (2005)

