 |
Gespanntes Seil vom Nordpol zum Südpol der Erde
Fragen und Bemerkungen gerne an: werner.brefeld@web.de, Adresse: siehe Impressum,
Themenübersicht auf der Hauptseite:
Mathematik im Alltag, verblüffende Mathematik-Rätsel, Stochastik und Polyeder, irdisches und außerirdisches Leben
|
28. Ein Seil wird straff vom Nordpol zum Südpol der Erde gespannt und anschließend
um 1 Meter verlängert. Wie weit kann man das Seil vom Erdmittelpunkt in Richtung Äquator ziehen, bis es wieder
straff wird, wenn man für den Radius der Erde eine Länge von 6378 km annimmt?
Bei diesem Mathematikrätsel handelt es sich natürlich um ein reines Gedankenexperiment. Dabei muss man
sich ein Loch vorstellen, dass vom Nordpol durch den Erdmittelpunkt zum Südpol reicht, und durch das man ein Seil spannen kann.
Außerdem muss man sich das Loch als hinreichend breit vorstellen, damit man das Seil nach der Verlängerung
wieder straff spannen kann.
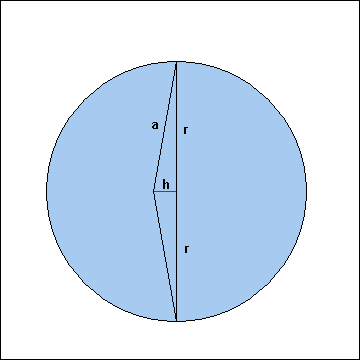
Bezeichnet man nun den Radius der Erde mit r, dann hat das Seil zu Anfang die Länge 2·r. Die Strecke, mit der
man das um 1 Meter verlängerte Seil ziehen kann, sei h.
Dann gilt nach Pythagoras die folgende Gleichung:
h2 + r2 = a2
Da 2·a die Länge des um s = 1 Meter verlängerten Seils ist, gilt außerdem:
2·a = 2·r + s oder a = r + 0,5·s
Nach Einsetzen von a in die erste Gleichung ergibt sich:
h2 + r2 = (r + 0,5·s)2
h2 = (r + 0,5·s)2 – r2
h2 = r2 + r·s + 0,25·s2 – r2
h2 = r·s + 0,25·s2
h2 = s·(r + 0,25·s)
h = √(s·(r + 0,25·s))
h erhält man dann durch Einsetzen der Werte für r und s:
h = 2525,470 m
Man kann das Seil also erstaunliche 2525,470 Meter in Richtung Äquator ziehen,
bis es wieder straff wird.
Was ist verblüffend an diesem Mathematik-Rätsel? Intuitiv glauben viele, nach einer Verlängerung
um nur einen Meter könne man das Seil nicht so weit in Richtung Äquator ziehen.
Solange die Seilverlängerung s klein ist im Vergleich zum Radius r einer Kugel, ist der Ausdruck
r + 0,25·s in guter Näherung gleich r. Deshalb kann man in so einem Fall auch die folgende
einfachere Näherungsformel benutzen:
h = √(s·r)
Für h erhält man wie oben den gleichen Wert von 2525,470 Meter. Die Abweichung zur exakten Formel ist also geringer als 1 mm.
Die Web-Seite Gespanntes Seil um den Äquator der Erde beschreibt ein ähnliches, aber schwierigeres Mathematikrätsel.
Copyright © Werner Brefeld (2008)

