 |
Lotto 6 aus 49 und die Strategie für überdurchschnittliche Lottoquoten
Fragen und Bemerkungen gerne an: werner.brefeld@web.de, Adresse: siehe Impressum,
Themenübersicht auf der Hauptseite:
Mathematik im Alltag, verblüffende Mathematik-Rätsel, Stochastik und Polyeder, irdisches und außerirdisches Leben
|
|
Mit welchen Lottozahlen erzielt man im Mittel überdurchschnittliche Lottoquoten beim Lotto 6 aus 49?
Welches sind die unbeliebtesten Lottozahlen?
Am Ende dieser Seite: Unbeliebte und beliebte Superzahlen!
Für Interessierte: Unbeliebte und beliebte Zahlen bei EuroJackpot
und EuroMillions
Zunächst soll einem verbreiteten Irrglauben entgegengewirkt werden. Die Wahrscheinlichkeit, mit einem Lotto-Tipp
einen Lottogewinn zu erzielen, kann man nicht durch das Ankreuzen bestimmter Lottozahlen erhöhen! Eine Lottokugel hat nämlich weder ein
Bewusstsein noch ein Gedächtnis und "weiß" deshalb nicht, ob ihre Lottozahl aus der Sicht der Menschen eine Glückszahl ist
oder ob sie in der Vergangenheit zu selten gezogen worden ist, also einen Rückstand hat. Nach 4900 Lottoziehungen ist z.B. jede
der 49 Lottozahlen im Mittel genau 600-mal gezogen worden. Angenommen, eine Lottozahl sei darunter, die durch Zufall 60-mal weniger, also nur
540-mal gezogen worden ist. Wie gleicht nun diese Lottokugel ihren zufällig entstandenen Rückstand von 10% wieder aus, obwohl sie nichts
davon weiß. Tatsächlich wird sie in Zukunft im Mittel genauso häufig gezogen werden wie die anderen. Wenn alle Lottozahlen also im Mittel
1200-mal gezogen worden sind, wird diese eine im Mittel 1140-mal gezogen worden sein. Sie ist also immer noch 60-mal seltener gezogen
worden. Allerdings liegt sie nun nicht mehr 10%, sondern nur noch 5% zurück. Obwohl sie also nicht häufiger gezogen worden ist als
die anderen Lottozahlen, ist der wichtige und entscheidende prozentuale Abstand kleiner geworden! So gleicht der Zufall also zufällig
entstandene Unterschiede wieder aus!
|
Dazu stelle ich eine kleine Auswertung der ersten eben erwähnten 4900 Lottoziehungen vor. Sie wurden am
16. Oktober 2010 erreicht. Jede Zahl sollte zu diesem Zeitpunkt im Mittel also 600-mal gezogen worden sein. Mit etwas Mathematik kann man ausrechnen,
wie viele Lottozahlen wie weit von diesem Mittelwert abweichen sollten, wenn nur der Zufall regiert. Die folgende Zusammenstellung zeigt,
wie viele Lottozahlen in welchen Häufigkeitsintervallen liegen sollten. In Klammern steht die tatsächlich gezogene Anzahl:
554-mal oder seltener: etwa 1 Lottozahl (1)
555-mal bis 577-mal: etwa 7 Lottozahlen (7)
578-mal bis 622-mal: etwa 33 Lottozahlen (32)
623-mal bis 645-mal: etwa 7 Lottozahlen (8)
646-mal oder häufiger: etwa 1 Lottozahl (1)
Man sieht, dass der Zufall ziemlich große Abweichungen erzeugt, und dass die tatsächlichen Lottoziehungen sich
sehr gut nur mit dem Zufall erklären lassen. Nur wenn die tatsächlichen Anzahlen deutlich von den erwarteten abweichen würden, sollte mit
den Lottoziehungen etwas nicht stimmen.
Die Gewinnchance pro Tipp kann man also beim Lotto nicht erhöhen. Anders sieht es mit der Lottoquote aus, die man erhält, wenn man denn einmal
gewonnen hat. In jeder Gewinnklasse wird nämlich ein bestimmter fester Anteil der gesamten Einspielsumme verteilt. Wenn also viele Lottospieler
mindestens drei der gezogenen Lottozahlen angekreuzt haben, wird das Geld unter entsprechend mehr Leuten aufgeteilt. Damit sinkt die
Lottoquote, die jeder Lottospieler erhält. Es kommt also darauf an, solche Lottozahlen anzukreuzen, die von den Mitspielern
eher gemieden werden. Dann wird die Geldsumme im Falle eines Gewinnes auf weniger Lotto-Tipps verteilt und die Lottoquote steigt.
Wichtig:
Leider kommt man auch durch das Ankreuzen der bei den Mitspielern unbeliebten Lottozahlen im Mittel nicht
in die Gewinnzone. Während alle Lottospieler durchschnittlich von jedem eingesetzten Euro etwa 50 Cent zurückbekommen, bekommt der geschickt
ankreuzende Lottospieler über alle Gewinnklassen gemittelt etwa 75 Cent zurück. Die Beliebtheit der Lottozahlen ist leider nicht unterschiedlich
genug, damit man im Mittel mehr Geld zurückbekommt als man eingesetzt hat. Wäre es anders, dann gäbe es diese Web-Seite nicht und ich würde
anfangen Lotto zu spielen.
Aber selbst wenn man im Mittel mehr Geld zurück bekäme als man eingesetzt hat, gibt es noch einen Haken. Da man selber nur ein Spieler ist,
der eben erwähnte Mittelwert aber für viele geschickte Spieler gilt, spielt noch die Wahrscheinlichkeit eine große Rolle, mit der man selber
diesen Mittelwert tatsächlich erreichen oder übertreffen würde. Diese Wahrscheinlichkeit ist aber verschwindend gering, weil ja alle
Gewinnklassen zum Mittelwert beitragen, man selber aber einen Gewinn in den obersten 3 Gewinnklassen mit größter Wahrscheinlichkeit
in seinem Leben nie bekommen wird.
Man kann also durch das Ankreuzen von unbeliebten Lottozahlen nur seine mittleren Verluste verringern. Deshalb sollte man auch nur dann
Lotto spielen, wenn man das entsprechende Geld übrig hat, wenn man also nicht auf die Gewinne angewiesen ist, und wenn der Spaß am
Lotto-Spiel größer ist als der Frust über das verspielte Geld. Diese Bedingung ist normalerweise überhaupt nur bei kleinen Geldbeträgen
und wenigen Einzel-Tipps (!) erfüllt. Damit man auch jederzeit ohne Probleme mit dem Lottospielen aufhören kann,
sollte man häufig seine Lottozahlen wechseln, weil man sich sonst immer an die in der Vergangenheit getippten Zahlen erinnern würde.
Unbeliebte und beliebte Lottozahlen
Wie findet man nun heraus, welche Zahlen unbeliebte Lottozahlen sind? Dazu berechnet man zunächst die theoretischen Lottoquoten für jede
Gewinnklasse unter Verwendung der jeweiligen Gewinnwahrscheinlichkeiten (siehe Web-Seite über Lottosysteme).
Diese Lottoquoten würden sich ergeben, wenn alle 139.838.160 möglichen Lotto-Tipps gleich häufig abgegeben worden wären. In die Berechnung geht ein,
dass nur 50% der Einspielsumme wieder ausgeschüttet wird. Außerdem muss die Aufteilung der ausgeschütteten Summe auf die verschiedenen Gewinnklassen
berücksichtigt werden. Weiterhin spielen die Wahrscheinlichkeiten eine Rolle, mit der ein Lotto-Tipp in den verschiedenen Gewinnklassen
einen Gewinn erzielt. Je kleiner die Wahrscheinlichkeit, desto größer die theoretische Gewinnquote. Und schließlich ist natürlich auch der Preis
pro Lotto-Tipp wichtig. Die folgende Berechnung der theoretischen Lottoquoten war bis zum 19.09.2020 gültig:
Gewinnklasse 1 (6 Richtige mit Superzahl): 50% · 12,800000% · 139.838.160 · 1€ = 8.949.642,20 €
Gewinnklasse 2 (6 Richtige ohne Superzahl): 50% · 73,962197% · 10% · 15.537.573 · 1€ = 574.596,52 €
Gewinnklasse 3 (5 Richtige mit Superzahl): 50% · 73,962197% · 5% · 542.008,4 · 1 € = 10.022,03 €
Gewinnklasse 4 (5 Richtige ohne Superzahl): 50% · 73,962197% · 15% · 60.223,2 · 1€ = 3340,68 €
Gewinnklasse 5 (4 Richtige mit Superzahl): 50% · 73,962197% · 5% · 10.324,0 · 1€ = 190,90 €
Gewinnklasse 6 (4 Richtige ohne Superzahl): 50% · 73,962197% ·10% · 1147,11 · 1€ = 42,42 €
Gewinnklasse 7 (3 Richtige mit Superzahl): 50% · 73,962197% · 10% · 566,56 · 1€ = 20,95 €
Gewinnklasse 8 (3 Richtige ohne Superzahl): 50% · 73,962197% · 45% · 62,951 · 1€ = 10,48 €
Gewinnklasse 9 (2 Richtige mit Superzahl): 50% · 13,237803% · 75,541237 · 1€ = 5,00 €
Liegen die tatsächlichen Lottoquoten einer Lottoziehung über diesen theoretischen Werten, müssen sich unter den gezogenen Lottozahlen welche befinden,
die unbeliebt sind und deshalb von den Spielern gemieden werden. Auf einer weiteren Web-Seite wird die Methode zur Berechnung der Beliebtheit der Lottozahlen erläutert.
Für die Berechnung wurden die 208 Lottoziehungen verwendet, die von Anfang 2018 bis Ende 2019 in Deutschland stattgefunden haben.
Für beliebte Zahlen ist die Beliebtheit größer als 1, für unbeliebte Zahlen liegt sie unterhalb von 1.
Wichtig: Seit dem 23.09.2020 beträgt der Einsatz pro Tippfeld 1,20 Euro und die Ausschüttungsanteile der Gewinnklassen haben sich geändert.
Eine Neuberechnung der Beliebtheiten der Lottozahlen kann wegen dieser Änderungen erst wieder ab etwa 2023 erfolgen. Allerdings ändern sich die Beliebtheiten
der Lottozahlen selbst über einen Zeitraum von 10 Jahren kaum, sodass die folgenden noch mit den alten Bedingungen berechneten Beliebheiten nach wie vor
das Tippverhalten der Spieler gut widerspiegeln.
Und hier sind alle Lottozahlen mit ihrer Beliebtheit:
| Lottozahl | Beliebtheit | Lottozahl | Beliebtheit |
Lottozahl | Beliebtheit | Lottozahl | Beliebtheit |
| | | | | | | |
| | | | | | | |
| | | | | | | |
| 43 | 0.807 | 34 | 0.885 | 2 | 0.989 | 32 | 1.089 |
| 14 | 0.816 | 22 | 0.909 | 49 | 0.992 | 10 | 1.110 |
| 35 | 0.829 | 28 | 0.914 | 23 | 0.993 | 18 | 1.115 |
| 36 | 0.833 | 40 | 0.920 | 41 | 1.008 | 26 | 1.117 |
| 44 | 0.855 | 1 | 0.926 | 13 | 1.023 | 6 | 1.126 |
| 45 | 0.857 | 48 | 0.933 | 27 | 1.036 | 5 | 1.131 |
| | | | | | | |
| | | | | | | |
| | | | | | | |
| 29 | 0.859 | 37 | 0.953 | 38 | 1.048 | 12 | 1.140 |
| 20 | 0.869 | 47 | 0.955 | 33 | 1.066 | 3 | 1.182 |
| 21 | 0.872 | 30 | 0.975 | 25 | 1.071 | 19 | 1.191 |
| 46 | 0.875 | 39 | 0.979 | 24 | 1.075 | 11 | 1.202 |
| 15 | 0.876 | 8 | 0.984 | 31 | 1.076 | 17 | 1.256 |
| 42 | 0.881 | 16 | 0.986 | 4 | 1.088 | 9 | 1.267 |
| | | | | | 7 | 1.337 |
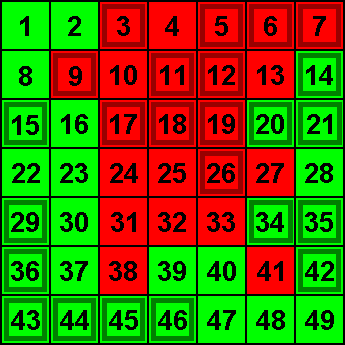
Im obigen Lotto-Tippfeld sind die 27 unbeliebten Zahlen grün und die 22 beliebten Zahlen rot markiert. Davon besonders hervorgehoben
sind die 13 unbeliebtesten Zahlen und die 11 beliebtesten Zahlen. Die 3 beliebtesten Zahlen sind die "Glückszahl" 7, die 9 und die 17.
Sie werden etwa 34%, 27% und 26% häufiger angekreuzt als dem Zufall entspricht. Diese 3 Lottozahlen sollte man auf keinen Fall
auswählen, wenn man im Falle eines Gewinns eine niedrige Gewinnquote vermeiden möchte.
Das Lotto-Tippfeld sieht aus, als hätten die Lottospieler einen "Brief" geschrieben. Oben befindet sich "Ort" und "Datum",
in der zweiten Zeile folgt die "Anrede", dann der "Text", schließlich der "Gruß" und darunter die "Unterschrift". Der linke
Rand bleibt frei, damit der "Brief" ordentlich aussieht. Bis auf die "Glückszahl" 7 bleiben auch der rechte
und untere Rand frei.
Wichtig:
Wie man außerdem erkennt, ist die oft aufgestellte Behauptung falsch,
dass sehr viele Lottospieler Geburtsdaten tippen und dass man deshalb alle Lottozahlen bis 31 meiden sollte. Tatsächlich sind
viele unter den ersten 31 Lottozahlen unbeliebt oder sogar sehr unbeliebt. Im Vergleich zu den "Briefe"-Tippern sind die
Geburtsdaten-Tipper also eine kleine Gruppe, die keinen nennenswerten Einfluss auf die Beliebtheit der Lottozahlen hat.
Man sollte nur unbeliebte Lottozahlen ankreuzen, wenn man im Mittel eine überdurchschnittliche Lottoquote
erzielen möchte. Dabei sollte man allerdings darauf achten, dass die sechs ausgesuchten Lottozahlen kein geometrisches oder
arithmetisches Muster bilden! Denn solche Muster sind bei vielen Lottospielern beliebt und führen trotz der angekreuzten
unbeliebten Lottozahlen zu schlechten Quoten. Außerdem sollte man für die Lotto-Tipps nicht nur die 6 oder 7 unbeliebtesten
Lottozahlen aus meiner Tabelle verwenden. Auf diese Idee könnten nämlich auch noch weitere Leser dieser Web-Seite kommen.
Die Enttäuschung im Falle von 6 Richtigen wäre dann groß.
Unbeliebte und beliebte Superzahlen
Genauso wie bei der Auswahl der Lottozahlen kommt es auch bei den Superzahlen darauf an, nur die Tippscheine mit den Superzahlen
zu verwenden, die von den Mitspielern eher gemieden werden. Dadurch würde im Falle eines Gewinnes zum Beispiel in der Gewinnklasse
"6 Richtige mit Superzahl" die Zahl der Mitgewinner im Mittel noch weiter verringert. Oft bekäme man sogar den Jackpot ganz alleine.
Für die Berechnung der Beliebtheit der Superzahlen wurden die 208 Lottoziehungen verwendet, die
von Anfang 2018 bis Ende 2019 stattgefunden haben.
Dabei wurde für jede Superzahl die Anzahl der Gewinner ermittelt, die sowohl genau drei Lottozahlen
als auch die Superzahl richtig hatten. Diese Zahlen wurden jeweils durch die Anzahl aller Gewinner dividiert, die bei der Ziehung der entsprechenden
Superzahl drei Lottozahlen richtig hatten. Das Zehnfache dieser Quotienten ergibt dann die entsprechende Beliebtheit.
Hier sind die 10 Superzahlen mit ihrer Beliebtheit:
| Superzahl | Beliebtheit |
| |
| |
| |
| 0 | 0,774 |
| 1 | 0,866 |
| 2 | 0,911 |
| 4 | 0,958 |
| 9 | 0,968 |
| |
| |
| |
| 3 | 1,048 |
| 8 | 1,050 |
| 6 | 1,085 |
| 5 | 1,121 |
| 7 | 1,202 |
Wie man erkennt, ist die 0 die unbeliebteste Superzahl. Sie sollte man auswählen, um möglichst wenige oder gar keine
Mitgewinner zu haben. Sollte man sich dazu nicht entschließen können, dann sollte man wenigstens die ausgesuchte Superzahl nicht auch noch als
Lottozahl ankreuzen. Das machen nämlich viele Spieler. Die beliebteste Superzahl ist die "Glückszahl" 7. Tippscheine mit dieser Zahl sollten Sie
auf jeden Fall meiden.
Im Durchschnitt vergehen übrigens etwa 29 Ziehungen, bis jede der 10 Superzahlen mindestens einmal gezogen worden ist (siehe Beispiel 20 auf der
Stochastik-Formeln-Web-Seite ("Überraschungseier-Problem")).
Und die Wahrscheinlichkeit, dass die Superzahl mit einer der 6 Lottozahlen übereinstimmt, beträgt 6/49 · 9/10 = 27/245 = 11,02%.
So ein Fall tritt also im Durchschnitt etwa alle 9 Ziehungen auf.
In der folgenden Abbildung sind unbeliebte Zahlen grün und beliebte Zahlen rot markiert. Besonders hervorgehoben sind die beiden unbeliebtesten
und die beiden beliebtesten Superzahlen.

Copyright © Werner Brefeld (1979; Originalquelle)


