 |
Der Wanderer und die drei Himmelsrichtungen
Fragen und Bemerkungen gerne an: werner.brefeld@web.de, Adresse: siehe Impressum,
Themenübersicht auf der Hauptseite:
Mathematik im Alltag, verblüffende Mathematik-Rätsel, Stochastik und Polyeder, irdisches und außerirdisches Leben
|
33. Ein Wanderer läuft erst einen Kilometer nach Süden, dann einen Kilometer nach
Osten und schließlich einen Kilometer nach Norden. Danach befindet er sich wieder am Ausgangspunkt.
Wo auf der Erde befindet sich dieser Ausgangspunkt?
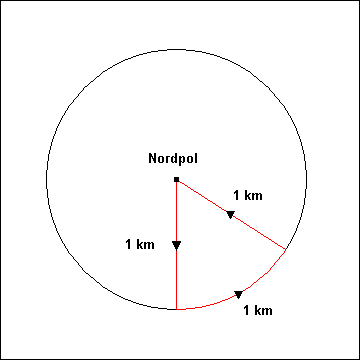
Der Nordpol erfüllt die im Rätsel genannten Bedingungen. Der Wanderer läuft also
vom Nordpol aus einen Kilometer nach Süden. Auf seinem Weg nach Osten muss der Wanderer einen Kreisbogen laufen,
weil eine Wanderung mit gleichbleibender Richtung immer mehr Richtung Süden führen würde. Da sich der Wanderer
auf dem Weg nach Osten immer genau einen Kilometer vom Nordpol entfernt befindet, führt ihn sein abschließender
Weg nach Norden zum Nordpol zurück. Die folgende Abbildung veranschaulicht den Wanderweg:
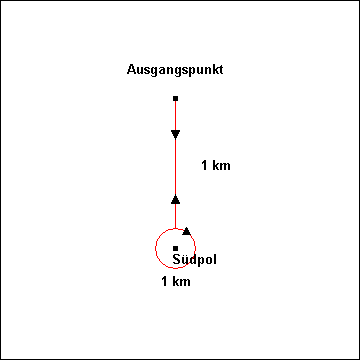
Der Südpol ist dagegen keine Lösung, denn vom Südpol aus kann man nicht nach Süden gehen. Man kann von hier zunächst nur nach
Norden gehen. Es gibt allerdings neben der oben beschriebenen Lösung noch weitere, und zwar unendlich viele. Sie befinden sich
alle in der Nähe des Südpols. Der Wanderer kann nämlich auch 1 km + (1 km / (2π)) = 1,159155 Kilometer
vom Südpol entfernt starten. Nachdem er einen Kilometer nach Süden gelaufen ist, befindet er sich dann nur noch
1 km / (2π) = 159,155 Meter vom Südpol entfernt. Dies entspricht dem Radius eines Kreises mit einem Umfang von
einem Kilometer. Der 1 Kilometer lange Weg nach Osten führt den Wanderer deshalb auf einem Kreis genau einmal um den
Südpol herum. Der Weg nach Norden bringt ihn dann wieder zu seinem Ausgangspunkt zurück. Es gibt überabzählbar unendlich
viele Ausgangspunkte, die 1 km + (1 km / (2π)) vom Südpol entfernt liegen, und daher entsprechend viele Lösungen.
Erstaunlicherweise gibt es zu jeder dieser unendlichen vielen Lösungen weitere unendlich viele Lösungen.
Der Ausgangspunkt kann sich nämlich auch 1 km + (1 km / (4π)) = 1,079577 Kilometer,
1 km + (1 km / (6π)) = 1,053052 Kilometer, 1 km + (1 km / (8π)) = 1,039789 Kilometer, usw. vom Südpol entfernt
befinden. Nachdem der Wanderer einen Kilometer nach Süden gelaufen ist, befindet er sich dann nur noch 1 km / (4π) = 79,577 Meter,
1 km / (6π) = 53,052 Meter, 1 km / (8π) = 39,789 Meter, usw. vom Südpol entfernt. Sein Weg nach Osten einmal um den Südpol
herum hat deshalb nur eine Länge von 1/2 km, 1/3 km, 1/4 km, usw. Der Wanderer muss also den Südpol zweimal, dreimal, viermal, usw.
umrunden, um auf einen Kilometer zu kommen, bevor ihn sein Weg nach Norden wieder zum Ausgangspunkt zurückbringt. Für die Entfernung
des Ausgangspunkts vom Südpol gibt es also ebenfalls unendlich viele Möglichkeiten, allerdings nur abzählbar unendlich viele.
Es sei noch erwähnt, dass die angegebenen Entfernungen zum Südpol zwar sehr genau, aber nicht exakt sind.
Der Südpol ist nämlich nicht der Mittelpunkt des geschlossenen Kreises mit einem Umfang von z.B. einem Kilometer,
weil die Erdoberfläche nicht eben, sondern kugelförmig gekrümmt ist. Dieser Effekt ist allerdings bei
Entfernungen von ungefähr einem Kilometer sehr klein.
Was ist verblüffend an diesem Mathematik-Rätsel? Intuitiv glauben zunächst viele, dass es für dieses Rätsel
keine Lösung gebe. Wenn sie dann schließlich den Nordpol als Lösung gefunden haben, sind sie davon überzeugt,
dass das die einzige Lösung sei.
Copyright © Werner Brefeld (2011)


