Dreieck aus Puzzleteilen mit Lücke? Fragen (werden beantwortet) und Bemerkungen gerne an: werner.brefeld@web.de Hier geht es zur Hauptseite mit den Themen: Mathematik im Alltag Verblüffende Mathematik-Rätsel Stochastik und Polyeder Irdisches und außerirdisches Leben

14. Werden in der abgebildeten Figur die vier Puzzleteile anders angeordnet, entsteht plötzlich eine Lücke. Ist die Gesamtfläche etwa kleiner geworden?

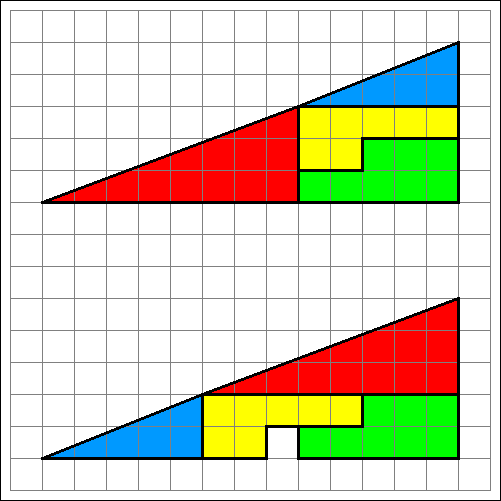
Dieser Eindruck beruht auf einer optischen Täuschung, weil entgegen dem Anschein weder die obere Figur ein Dreieck noch die untere Figur ein Dreieck mit Lücke ist. Die obere "Seite" knickt bei der ersten Figur im mittleren Bereich nach oben und bei der zweiten Figur nach unten. Man kann leicht nachrechnen, dass die Steigungen der beiden betroffenen Puzzle-Stücke nicht gleich sind. Das linke Puzzle-Dreieck bei der oberen Figur ist 8 kleine Quadrate breit und rechts 3 kleine Quadrate hoch. Die Steigung dieses Dreiecks ist demnach 3/8 = 0,375. Das rechte Puzzle-Dreieck ist 5 Quadrate breit und rechts 2 Quadrate hoch. Hier beträgt die Steigung also 2/5 = 0,400 und ist somit größer. Bei der unteren Figu sind die Verhältnisse genau umgekehrt und das Dreieck mit der größeren Steigung liegt links. Dadurch wird hier mehr Fläche verbraucht, die an anderer Stelle durch eine entsprechende Lücke wegen der Flächenerhaltung wieder eingespart werden muss. Der Knickwinkel in beiden Figuren beträgt jeweils 1,245°.

Auch durch eine Flächenberechnung kann man die Täuschung aufdecken. Die beiden Puzzle-Dreiecke haben eine Fläche von 8 · 3/2 = 12 bzw. 5 · 2/2 = 5 Quadrate. Die beiden übrigen Teile sind 7 bzw. 8 Quadrate groß. Zusammen beträgt die Fläche also 32 kleine Quadrate. Wären die obere Figur wirklich ein Dreieck, dann betrüge seine Fläche aber 13 · 5/2 = 32,5 kleine Quadrate. Durch Vergleich erkennt man auch hier, dass etwas nicht stimmen kann.


Was ist verblüffend an diesem Mathematik-Rätsel? Intuitiv halten wir die beiden Figuren für ein Dreieck bzw. für ein gleich großes Dreieck mit Lücke, obwohl uns der Verstand sagt, dass die beiden Flächen gleich sein müssen.


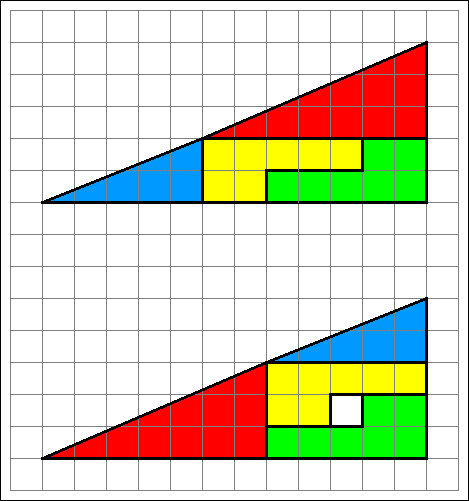
Die folgende Abbildung zeigt eine zweite Variante dieses Rätsels. Der Knickwinkel ist mit 1,298° nur unwesentlich größer. Dafür sind sogar zwei Puzzleteile gleich.




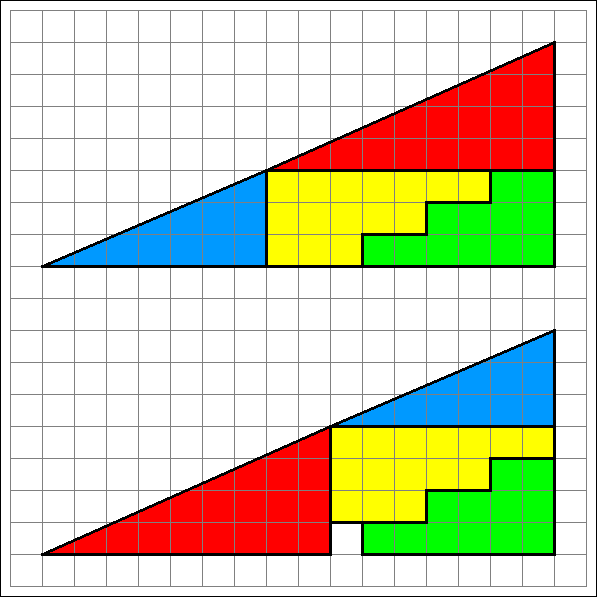
Die letzte Abbildung zeigt schließlich eine Figur, bei der der Knickwinkel nur noch 0,764° beträgt. Der Knick ist also noch schwerer zu erkennen als bei den beiden oberen Figuren.




Copyright © Werner Brefeld, 2005 ... 2012